(If you like this, you should check out my cartoons on YouTube and my mailing list.)
Computer science is what enables programming, but it is possible to do a lot of programming without understanding the computer science concepts underlying the process of computation. This isn’t always a bad thing. When we program we work at a much higher level of abstraction. When we drive a car, we only concern ourselves with two or three pedals, a gearshift, and a steering wheel. You can safely operate a car without having any clear idea of how it works. However, if you want to operate a car at the very limits of its capabilities, you need to know a lot more about automobiles than just the three pedals, gearshift and steering wheel.
The same is true of programming. Much mundane everyday work that can be accomplished with little or no understanding of computer science. You don’t need to understand computational theory to build a “contact us” form in PHP. However, if you plan to write code that requires serious computation, you are going to need to understand a bit more about how computation works under the hood.
The purpose of this article is to provide some fundamental background for computation. If there is interest I may follow up with some more advanced topics, but right now I want to look at the logic behind one of the simplest abstract computational devices–a finite state machine.
Finite State Machine
A finite state machine is a mathematical abstraction used to design algorithms. In simple terms, a state machine will read a series of inputs. When it reads an input it will switch to a different state. Each state specifies which state to switch for a given input. This sounds complicated but it is really quite simple.
Imagine a device that reads a long piece of paper. For every inch of paper there is a single letter printed on it–either the letter a or the letter b.
As the state machine reads each letter it changes state. Here is a very simple state machine.
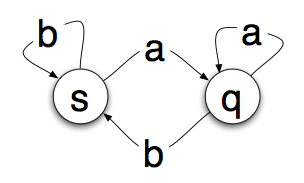The circles are “states” that the machine can be in. The arrows are the transitions. So if you are in state s and read an a you’ll transition to state q. If you read a b, you’ll stay in state s.
So if we start on s and read the paper tape above from left to right, we will read the a and move to state q. Then we’ll read a b and move back. Another b will keep us on s followed by an a which moves us back to the q state. Simple enough, but whats the point?
Well it turns out that you can run a tape through the state machine and once it is done tell something about the sequence of letters by examining the state you end up on. In our simple state machine above, if we end on s, the tape ends with the letter b, if we end on q, the tape ends with the letter a.
This may sound pointless, but there are an awful lot of problems that can be solved with this type of approach. A very simple example would be to determine if a page of HTML contains these tags in this order:
<html> <head> </head> <body> </body> </html>
The state machine can move to state that shows it has read the html tag, loop until it gets to the head tag, loop until it gets to the head close tag, etc. If it successfully makes it to the final state, then you have those particular tags in the right order.
Finite state machines can also be used to represent the mechanics of a parking meter, pop machine, automated gas pump and all kinds of other things.
Deterministic Finite State Machine
The state machines we’ve looked at so far are all deterministic state machines. From any state there is only one transition for any allowed input. In other words there aren’t two paths leading out of a state when you read the letter a. At first this sounds silly to even make this distinction.
What good is a set of decisions if the same input can result in moving to more than one state? You can’t tell a computer, if x==true then execute doSomethingBig or execute doSomethingSmall, can you?
Well you kind of can with a state machine. The output of a state machine is its final state. It goes through all its processing and then the final state is read and then an action is taken. A state machine doesn’t do anything as it moves from state to state. It processes and then when it gets to the end, the state is read and something external triggers the desired action (dispenses a soda can, etc.). This is an important concept when it comes to non-deterministic finite state machines.
Non-deterministic Finite State Machine
Non-deterministic finite state machines are finite state machines where a given input from a particular state can lead to more than one different state. For example, lets say we want to build a finite state machine that can recognize strings of letters that start with a and are then followed by zero or more occurrences of the letter b or zero or more occurrences of the letter c terminated by the next letter of the alphabet. Valid strings would be:
- abbbbbbbbbc
- abbbc
- acccd
- acccccd
- ac (zero occurrences of b)
- ad (zero occurrences of c)
So it will recognize the letter a followed by zero or more of the same letter of b or c followed by the next letter of the alphabet. A very simple way to represent this is with a state machine that looks like the one below, where a final state of t means that the string was accepted and matches the pattern.
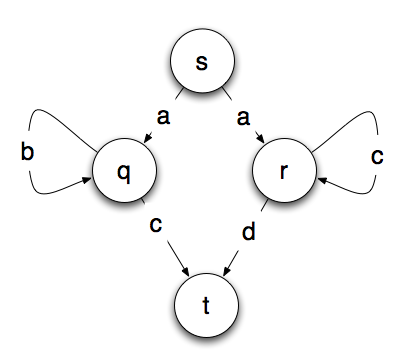Do you see the problem? From starting point s, we don’t know which path to take. If we read the letter a, we don’t know whether to go to the state q or r. There are a few ways to solve this problem. One is by back tracking. You simply take all the possible paths and ignore or back out of the ones where you get stuck.
This is basically how most of the chess playing computers work. They look at all the possibilities and all the possibilities of those possibilities and choose the path that gives them the greatest number of advantages over their opponent.
The other option is to convert the non-deterministic machine into a deterministic machine. One of the interesting attributes of a non-deterministic machine is that there exists an algorithm to turn any non-deterministic machine into a deterministic one. However, it is often much more complicated. Fortunately for us, the example above is only slightly more complicated. In fact this one is simple enough we can transform it into a deterministic machine in our head without the aid of a formal algorithm.
The machine below is a deterministic version of the non-deterministic machine above. In the machine below, a final state of t or v is reached by any string that is accepted by the machine.
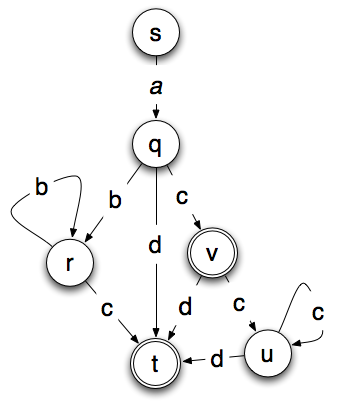
The non-deterministic model has four states and six transitions. The deterministic model has 6 states, 10 transitions and two possible final states. That isn’t that much more, but the complexity usually grows exponentially and a moderately sized non-deterministic machine can produce an absolutely huge deterministic machine.
Regular Expression
If you have done any type of programming, you’ve probably encountered regular expressions. Regular expressions and finite state machines are functionally equivalent. Anything you can accept or match with a regular expression can be accepted or matched with a state machine. For example the pattern above could be matched with:
a(b*c|c*d)
Regular expressions and finite state machines also have the same limitations. In particular they both can only match or accept patterns that can be handled with finite memory. So what type of patterns can’t they match? Lets say you want to only match strings of a and b, where there are a number of a’s followed by an equal number of b’s. Or n a’s followed by n b’s where n is some number. Examples would be:
- ab
- aabb
- aaaaaabbbbbb
- aaaaaaaaaaaaaaaaaaaabbbbbbbbbbbbbbbbbbbb
At first this looks like an easy job for a finite state machine. The problem is that you’ll quickly run out of states or you’ll have to assume an infinite number of states–at which point it is no longer a finite state machine. Lets say you create a finite state machine that can accept up to 20 a’s followed by 20 b’s. That works fine until you get a string of 21 a’s followed by 21 b’s at which point you will need to rewrite your machine to handle a longer string. For any string you can recognize, there is one just a little bit longer that your machine can’t recognize because it runs out of memory.
This is known as the Pumping Lemma which basically says, if your pattern has a section that can be repeated like the one above then the pattern is not regular. In other words neither a regular expression nor a finite state machine can be constructed that will recognize all the strings that do match the pattern.
If you look carefully, you’ll notice that this type of pattern where every a has a matching b, looks very similar to HTML where within any pair of tags you may have any number of other matching pairs of tags. So while you may be able to use a regular expression or finite state machine to recognize if a page of HTML has the html, head and body elements in the correct order, you can’t use a regular expression to tell if an entire HTML page is valid or not because HTML is not a regular pattern.
Turing Machines
So how do you recognize non-regular patterns? There is a theoretical device that is similar to a state machine called a Turing Machine. It is similar to a finite state machine that it has a paper strip that it reads, but a Turing Machine can erase and write on the paper tape. Explaining a Turing Machine will take more space that we have here, but there are a few important points relevant to our discussion of finite state machines and regular expressions.
Turing Machines are computationally complete and anything that can be computed can be computed on a Turing Machine. Since a Turing Machine can write as well as read from the paper tape, it is not limited to a finite number of states. The paper tape can be assumed to be infinite in length. Obviously, actual computers don’t have an infinite amount of memory, but they contain enough memory that you don’t hit the limit for the type of problems they process.
Turing Machines give us an imaginary mechanical device that lets us visualize and understand how the computational process works. It is particularly useful in understanding the limits of computation. If there is interest I’ll do another article on Turing Machines in the future.
Why does this matter?
So whats the point? How is this going to help you create that next PHP form? Regardless of their limitations state machines are a very central concept to computing. In particular, the recognition that for any non-deterministic state machine you can design, there exists a deterministic state machine that does the same thing. This is a very key point because it means you can design your algorithm in whichever way is the easiest to think about. Once you have a proper algorithm, you can convert it into whatever form is most efficient.
The understanding that finite state machines and regular expressions are functionally equivalent opens up some incredibly interesting uses for regular expression engines–particularly when it comes to creating business rules that can be changed without recompiling a system.
A foundation in computer science allows you to take a problem X that you don’t know how to solve and reason, “I don’t know how to solve X, but I do know how to solve Y and I know how to convert a solution for Y into a solution for X. Therefore I now know how to solve X.”
(If you like this article, you might enjoy my YouTube channel where I create an occasional video or cartoon about some aspect of creating software. I also have a mailing list for people who would like an occasional email when I produce something new.)
I think there is an error in the “fixing” of the non-deterministic state machine case?
Legal is s -a-> q -c-> t and yet your “fix” would take s -a-> q -c-> v
Good catch. The non-deterministic machine accepts a(b*c|c*d) (ad is valid) while the deterministic machine accepts a(bb*c|cc*d) (there must be at least 3 different letters).
Thanks for pointing this out. I have updated the deterministic machine to make it match the non-deterministic one.
Where you write “a number of a’s followed by a number of b’s”, it would be clearer to say “followed by an equal number…”
Thanks for the suggestion. I’ve incorporated it.
Your regular expression could make use of the + operator: a(b+c|c+d) would be more better, if only by a few bytes….
Good suggestion. I started to do that, but I couldn’t remember if the + sign was allowed in formal proofs or not. Not that this article is particularly formal….
There’s no reason “+” should be barred. “a+” is trivially equivalent to “aa*”
That is why I was thinking it wasn’t allowed–it is redundant.
Just the spelling and grammar errors. For now we will refrain from pointing out the 10-12 missing commas, depending on the editor’s love of commas.
When it reads and input it will switch to a different state.
When it reads an input it will switch to a different state.
The state machine can move to state the shows it has read the html tag,
The state machine can move to a state that shows it has read the html tag,
In other words their aren’t two paths leading out of a state when you read the letter a.
In other words there aren’t two paths leading out of a state when you read the letter a.
If we read the letter a, we don’t know wether to go to the state q or r.
If we read the letter a, we don’t know whether to go to the state q or r.
So how to you recognize non-regular patterns?
So how do you recognize non-regular patterns?
I appreciate the constructive feedback and have corrected those errors. Thank you!
you missed:
“Therefore I now known how to solve X.”
should be:
Therefore I now know how to solve X.
Thanks!
I believe your example for pumping lemma is incorrect. You can represent any number of “a” followed by any number of “b” as a*b*
That should’ve been _n_ number of “a” followed by _n_ number of “b”.
The wording may have been slightly ambiguous, but the idea is correct.
The regular expression you’ve given would match input such as “aaaabb”, whereas the machine is intended to only accept input consisting of a number of a’s followed by the *same* number of b’s. I don’t believe you can express this with the Kleene star (*).
It’s a common example of the pumping lemma problem.
I got confused at
“a number of a’s followed by a number of b’s”
would this a any more clearer:
“a number of a’s followed by the same number of b’s”
I agree. The wording is ambiguous. I’ve made the change.
I think example with HTML is bad one, because reader can get an illusion that HTML can be checked with Finite State Machine. But it can’t, since that HTML document can have infinite depth. I know that you pointed to only that particular case, but still.
I see your point. I was trying to find a way to illustrate how state machines can be used to do some things with html. But I agree it is confusing. I’ll try to find a different example.
A SAX Parser is a finite state machine. If you don’t mind qualifying your example as using XHTML, or switching to a generic XML example, it should illustrate what you want nicely. (Ready) -> startElement -> (Parsing) -> endElement -> (Done)
(Need to add a !endElement input from Parsing to transition back to itself, but I can only do so much with ASCII)
It’s also a nice example of using state machines in recursion, since the Parsing state should invoke a new instance to capture each child element.
A SAX parser is a finite state machines, but it is not capable of accepting all valid XHTML any more than a regular expression. What you’ve described will stop working when you run out of memory.
But yes for practical purposes a SAX parser is a finite state machine that accepts a subset of the documents that are valid XHTML.
You have a mistake in your deterministic translation of the non-deterministic FSM. The non-deterministic one accepts ACD as an input, yet the deterministic version requires at least a second C (ACCD, minimally). Adding a transition from v to t on D would fix this.
Ah thank you. I tried to correct one error and introduced another. :) How does it look now?
The state ‘u’ is extraneous now. The loop following ‘c’ from ‘u’ to ‘u’ can be a loop following ‘c’ from ‘v’ to ‘v’ instead (mirroring the state ‘r’ on the other side).
I’m pretty sure I need ‘u’. Keep in mind that ‘v’ is a final state. ‘ac’ is valid, but ‘acc’ is not valid and must be followed by ‘d’. That is what ‘u’ does. It keeps the machine from accepting ‘acc*’.
I had to go over this one as well, initially agreeing with K.M., but indeed Mark is right. But it takes some thought (at least for an untrained ‘state’ mind)
My vote as well for a followup article!
Several statements in your post are contradictory. The second sentence in the “Non-deterministic Finite State Machine” states the example to “start with a and are then followed by one or more occurrences of the letter b or one or more occurrences of the letter c …”. The examples of valid strings include “ac (zero occurrences of b)” and “ad (zero occurrences of c)”. Zero occurrences is not “one or more”.
The state diagram shown will accept zero “b”s or “c”s, but the description again states “one or more …”
Thank you. I believe I have fixed the error.
You fixed the one in the first paragraph, but not in the description of the state diagram.
I’m a bit confused? If you know that there will always be the same number of a’s as there are b’s couldn’t you have a state machine increment a number for ever a it comes across?
Or am I not thinking about it correctly?
A state machine can’t write anything down. It only has a finite number of states. Once you start writing a number down, you have infinite number of states because there are infinite numbers.
Tony: your question is a good one. As Mark said the finite state machine can’t write anything down. Another machine that could, however, “remember” the context (how many a’s have been encountered, and expect the same number of b’s) is something called a push-down automata. For your information, a push-down automata basically adds a First-In-Last-Out stack to the Finite State Machine.
Mark: Your article was a good one, and I enjoyed reading it. Will you do the intermediate machine on your way to Turing Machines, or will you jump directly to Turing Machines? I would love to see your description of Push-Down Automata Machines.
Thats a good suggestion. It would also be interesting to talk more about how regular expressions can be converted to state machines and how you can combine state machines to create the union, complement and intersection of accepted strings. Then there is the whole state minimization algorithm and non-deterministic to deterministic algorithm that would be interested to get into.
Unfortunately most of those topics would get away from the physical mechanical models and I’m not sure it would be as interesting for people to read, but maybe we’ll have to experiment and see what people think.
Thanks for your encouragement to write more.
I might be wrong, but it seems like the regular expression “a(bb*c|cc*d)” does not support the valid string “ac”?
No you are right. I corrected some errors in one place and forgot to change it there. Thanks!
I’ll be the first to say today then, well done on the article, very informative. Thanks!
Thanks for the clear and concise explanation. Would love to read your explanation of Turing machines.
Thanks. I hope to write an article about Turing machines in the near future.
Another vote for the Turing machine article. There is demand :)
Great article. Thanks for it. What’s a good book to pick up to learn more? I have a good grasp of programming, but a weak understanding of theoretical CS.
Bob, the book used in our undergraduate courses on Automata and Languages, Computability Theory and Complexity Theory is the excellent “Introduction to the Theory of Computation” by Michael Sipser.
Your article is well written (despite a few grammatical errors), and your explanation of finite state (deterministic and non-deterministic) is both accurate and easily understandable. My only objection is that you have jumped from finite state machines and regular grammars directly to Turing machines. The example of a^nb^n is actually a context free grammar and the corresponding machine model is a pushdown automata (basically a finite state machine with a stack attached) both models are simpler than the lambda calculus (for example) and the Turing machine.
I see your point. My goal wasn’t to really explain Turing machines, but just to introduce the notion that there are machines that will allow you to do the things that you cannot do with a finite state machine.
However, you are correct, the state machine with a stack is going to be a better match for parsing something like HTML and a^nb^n which I used as an example.
Thanks for your input.
This is a great article. Another vote for the Turing machine article from me!
Well, nice article. I am confused by the comments, though. Are only theoretical scientists reading this blog? I haven’t seen this level of constructive criticism … I think ever, maybe excepting science paper reviews :)
In my college I had found Theory of Computation to be most bland topic. But the way you have elucidated it deserves plaudit . look forward to your other articles
Thank you for this article. I’ll be waiting for your Turing Machines one.
Thanks for the easy consumable information, I would appreciate more detailed information!
I have always wandered about State Machines & Turing Machines. I have flipped through wikipedia several times but never really understood them as wikipedia articles are bloated and hard to understand. Thanks for the lucid explanation. ;)
Just a quick note: using FSMs built using statecharts (instead of character sequences) is often more intuitive if you’re teaching someone the material for the first time (more so if they have no cs education).
Fundamentally there’s no difference, but in practice there is a different flavor. In particular a design pattern for making robust GUIs is to code up a statechart fsm for the possible states, like no file, file loading, file active, file changed, file saving, file closing, etc., and callbacks for handling state transitions.
As one of those people who programs every day without understanding the underlying fundamentals, I appreciated this article. It was easy to follow and I came away with a bit more of the “why” of what I’ve been doing. Thank you!
Mark,
I appreciate you taking this task on. It was informative and helpful. I am looking forward to more on the Turing machine concept. I guess you found that the people that are into this stuff are a little OCD (typo: a LOT OCD :-).
Thanks again,
John
Thanks. I’ve appreciated everyone’s feedback. This is the type of thing where if you aren’t OCD it can be very confusing. I learned a long time ago that if I wait to publish an article until it is perfect, it will never get posted, so I’m very glad for all the suggestions.
People Found This When Looking For:
* custard eating hobos in flower dresses (124)
What’s with this????
Someone is messing with me by doing searches that will return this page, but with bogus terms added in. They iterate until they can do a search with only the bogus terms. I least I think that is what is happening. They may just be spoofing the referrer header. :)
Thanks for the article, Mark. I found it very easy to follow and very interesting.
Excellent article, very informative for someone who doesn’t have a CS degree. I hope to see a follow up article on Turing Machines….
I love the phrase “custard eating hobos in flower dresses” although I think a hyphen should separate “custard” and “eating”.
But what in the world is the significance/origin of it? Is it a quote from something/somewhere, an inside joke, a clever-clever trick, or…?
I have no idea.
Ah, I remembered the good old days at college with this topic. I totally agree, it’s important to understand how things work. For instance, you might never get to write code in assembly, but knowing assembly gives you an understanding of why higher languages like C or C++ work the way they do, and you become a better programmer ;)
Thank you for your article. I am studying programming without basic computer science understanding. At least, by reading your article, I have some directions to follow next.
Turing machines aren’t as useful in programming as one might think — they’re a model of computation that lets you reason on what is and isn’t computable. If you’re building a turing machine into your program, you’re very likely doing it wrong.
Far better to follow up the FSM article with something like an article on pushdown automata, Moore machines, Mealy machines, etc.
Also, you did manage to miss (or I did) one of the truly wonderful things about FSMs — how very simple the representation is. The five-tuple (alphabet, set of states, set of terminal states, start state, and transition table) is a simple way to organize what may end up being something quite complicated under the covers.
(If for nothing else, it can help drive home the distinction between data structures and data, especially for those programmers who have the belief that complicated data requires complicated data structures.)
Thanks. I would be interested in the Turing Machine article. I like your addition of diagrams to the descriptions; They definitely help me conceptualize what you’re describing.
Thanks for your article! I’m looking forward to the Turing Machine one.
sir plz guide me about this
Construct deterministic Finite State Automata for each of the following over
Σ = {x, y}:
a. Language of all those strings in which second last symbol is ‘y’.
b. Language of all those strings whose length is odd and number of y’s is even.
A nice article, would read more with great pleasure. Probably more on regular expressions. Your explanations are really simple to understand.
What do you meen by
” finite state machines and regular expressions are functionally equivalent opens up some incredibly interesting uses for regular expression engines–particularly when it comes to creating business rules that can be changed without recompiling a system.”?
I was trying to point out that anything that you want to represent as a state machine (business rules, etc.) can also be represented as a string that is a regular expression. So if you have something in your language that can execute a string that is a regular expression, you could use that to create business rules at run time that could be executed (using the regular expression engine) without needing a recompile.
At least I think that was what I was trying to point out when I wrote it.
Great insight, which caused some sort of eureka moment. Thanks for a great article, and in particular thanks for this specific example!
Thank you very much for writing this article.
I am new to the concept of finite state machines, and the ones I found on Wikipedia were giving me migranes…
Great article, THANKS for it! I used to design space electronics for Hughes, TRW and Ball Aerospace. I found out about state machines from an article by Christopher Claire in Electronics magazine about 1970 or so. Microprocessors were pretty primitive then, and we just needed something to control a space instrument or provide timing and control for a CCD camera, so nothing too complicated. I found state machines were just the ticket — I could scribble out a flow chart, run it by the rest of the crew (even managers could understand it), incorporate their suggestions, and design the SM from the flow chart — in MINUTES. I just used a counter, decoder, mux and combinatorial logic to create the ‘jump states’ which were ‘jams’ to force the counter to go to another, not the next sequencial, state. Where the 8051 microprocessor programmers would spend weeks getting their code to work, I could pump out a SM design during the kick-off meeting! It was great fun, and I taught all the young designers how to do it in no time. Ball Aerospace in Boulder, CO was NASA’s go-to place for quick jobs into space, and we all were having a blast doing it — a lot of that was due to the lowly state machine.
The image links are broken. I need to delete one letter from the domain for them to appear.
Otherwise, this is an article that I would like to share with my students.
Thanks for pointing that out. It should work now.
Interesting article, thanks.
But one practicality puzzles me: in the deterministic chart, v is a valid endpoint (as shown by the double circle) since ac is a valid string. But it’s an endpoint that’s also a waypoint, since acc and acd are valid as well.
So how do you implement that in a practical sense? If it was a program waiting for characters over a serial interface for example, would you implement some kind of timeout at state v, at which point you would say “ok, looks like we’re not getting any more c’s or a d so we’ll stop now”?
Obviously, it depends on what the input actually is. If you are reading a paper tape, once you run out of paper you can stop looking for more. If your application is a server and someone connected to it, maybe the termination of the connection means you can stop looking for additional input. Alternatively, the statemachine may just be used to determine if some other action can take place, so there may be some other process that is looking to see if the statemachine has accepted it’s input to determine if it is allowed to continue or not. For example, the statemachine might be used to determine if the submit button is active on a web page.
Why do we need “u” state in the deterministic state machine ? And why there is 2 final states?
Try to remove “u” and run some of the sample strings through it. You’ll find you can’t handle some of them without having it. There are two ending states because valid strings can end in c or in d and there isn’t a way to handle both of those situations with a single end state–at least not that I was able to find.
Is it correct to say that a state machine is not really a machine for keeping track of state in but a an algorithm for computing an answer? I.e., it’s not that if I need to build a workflow tracking app I should expect that I will build a finite state machine? I am thinking this because you show it not as something that maintains state over time but as something that computes and answer like a regular expression.
To the extent that the answer being computed is whether or not a string is accepted by the state machine, yes. :) The thing that is interesting about state machines is that they can accept or reject arbitrarily long strings without requiring any type of memory. Other types of machines (pushdown automata for instance) can only operate as long as they don’t run out of memory.
You can use a state machine to represent the stages of a workflow tracking app, but if you want the history of all the different states a piece of work has been in, then a raw state machine isn’t going to work for you. A state machine can tell you if you end in a desired state or not, but it can’t tell you what path was taken to get to that state. This might not be what you want for a workflow app. You are correct that state machines are computationally equivalent to regular expressions.
Hey there Mark i really appreciate your article, but I got lost with the graph – i couldn’t quite follow it.
What part was confusing?
Thanks for this nice article.
Now I’m wondering if the non-deterministic state machine is the idea behind quantum computers? Not sure if it makes sense.
If I understand what you are thinking, I don’t think so. Although you might be able to try to represent quantum state using a state machine, but I’m not sure what that would gain you.
Thanks for your time to write this article, I find this simple and useful, I am writing about deterministic finite state machines concepts to program PLCs.
Thank you for the article!
Hello Mark.
An excellent article! Very much appreciated.
On my understanding, the patterns that can be recognized by state machines are regulares or non-regulares. Is that it? What’s the difference between these patterns?
Thanks!
The patterns that can be recognized by state machines are the same as what can be recognized by regular expressions. Regular patterns are patterns that can be identified without needing to keep track of something in memory. For example the pattern abababab… (however many repetitions) is regular because it just requires two states, but the letter a repeated n times followed by the letter b repeated n times is not regular because you need some way to keep track of how many a’s you’ve seen in order to compare them to the number of b’s you see later.
Does that help?
Thank you for the excellent article. I have a question about turning non-deterministic state machine into a deterministic one. Why is the diagram above “Regular Expression” considered deterministic? There are still two paths leading out of state q, and both paths can lead to state t.
Thank you!
A non-deterministic state machine will have two transitions out of one state where the same input (say the letter ‘a’) can lead to two different states. In the diagram you referenced, there are multiple states leading out of q, but each one is for a different input. It is deterministic in the fact that you never have to guess which path to take for a given input.
Does that help?